MC Digital プログラミングコンテスト2023(AHC019)参加記
自分にしてはまたいい順位が取れたというのと、比較的上位寄りの人で解法が被っていなさそうだったので書きました。図を書く余力がなくて文字ばっかりになってしまったので、わかりづらいかもしれません…
問題
結果

Pretest / System Test ともに 21位 / 738 でした。問題を読んだ時の印象から考えるといい順位だったので嬉しかったです!
解法
準備
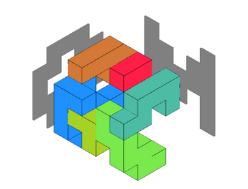
上のように正面・右側のシルエットの組とその投影前のブロックが置ける空間のことをまとめて、本記事では「シーン」と名付けています。
要約
- Monte Calro Tree Search (MCTS) を使って、各シーンに共通のブロックを置いていく乱択貪欲を時間いっぱい繰り返しました。
- MCTS のノードは共通のブロックの作り方を表していて、0-indexed で 0 段目をroot とすると、奇数段目で共通ブロックの開始位置とブロックの方向、偶数段目でブロックの大きさを調節します。
- 共通ブロックの作り方は、BFS で出来る限りサイズを大きくしてシルエットを埋めていき、シルエットが全部埋まった後で小さいブロックを逐次的に膨らませます。
- 他にも、貪欲としてプレイアウトの質を高めるための工夫をしたり、MCTS の子ノードを展開する数を減らすためにいろいろ工夫しました。
ベースとなる乱択アルゴリズム
大まかに、①シーン内のシルエットを全て埋める、②小さいブロックの体積を増やす、の流れです。
まず、各シーンで共通のブロックを一つずつ配置していきます。ブロックの配置を決めるためには、具体的には以下の4つを決めます。
- シーン1のブロックの開始位置
- シーン2のブロックの開始位置
- シーン1内のブロックに対してシーン2内のブロックが向く方向
- ブロックの体積
それらをランダムに決めたうえで、各ブロックの開始位置から BFS で共通ブロックを切り出していき、上で定めた指定の体積になるまでブロックを拡大していきます。
次に、①を繰り返して両シーンの全てのシルエットが埋まった段階で、体積が最も小さいブロックを選択して体積を適当に1増やすという操作を、ブロックの体積増加ができなくなるまで繰り返します。これは、小さいブロックの体積を増やすことがスコア上昇に大きく寄与するためです。
以上の2ステップを時間いっぱい繰り返す乱択がベースのアルゴリズムです。
MCTS を使う動機
探索を行う際にそれまでの探索で得た良い形を保存したいです。完全な乱択アルゴリズムだとそれができないけど局所探索ではできるので、このままだと局所探索より性能として劣ってしまいそうです。そこで、せめて最初の方に置いたブロックが結果的に良かったのかを判断していい形として保存するためにMCTS を採用しました。
特に今回のように制約が厳しい問題では、期待値としていいスコアが出ることと最良スコアが更新できることは分けて考えた方がいいとは思うのですが、根本的な解決方法がわからないうえに結果としてただの乱択貪欲よりはスコアが出たのでそのまま採用しました。こういう雑ないい状態の保存方法ではブロックの調整を行うなどは狙ってできないので意図的に設計したアルゴリズムのスコアに到達するのは難しいとは思いますが、どうやっても局所探索できるイメージが湧かなかったので諦めるしかなかったです。
MCTS を使う上での課題
今回対策した範囲でいうと、大きく2つあります。
1つ目に、ベースとなる乱択アルゴリズムではブロックを切り出すために4つの情報を決める必要があり、これをそのまま MCTS のノードとして持たせると明らかに子ノードの数が多すぎて性能が出ません。MCTS を実行するには各子ノードで最低でも1回はプレイアウトを行う必要があるので無駄な探索を含んでしまいそうですし、特定ノードで行うプレイアウトの回数もある程度積まないと ucb1 等のスコアが意味をなさなくなるので、できるだけ子ノードの数を減らす必要があります。
2つ目に、単純な乱択で良いスコアを出すためにはランダムに生成したブロックの全てについて正しい置き方をする必要があり、良い解を作る観点では分が悪いです(極端な話でいうと、何か一つブロックの体積をランダムに1と選択すると、それだけでスコアが悪化する)。少し余計に時間がかかったとしてもプレイアウトの質を何らかの意味で高める必要があります。
工夫の一覧
ブロックの方向をシルエット被覆面積が多い1方向に限定
ブロックを置くために決める情報のうち「シーン1内のブロックに対してシーン2内のブロックが向く方向」は24パターンありますが、そのうち限界まで大きいブロックを作った際のシルエットが被覆できる面積が多いものだけを選択しました。動機としては、被覆面積が多いほどブロックの個数が少なくプレイアウトを終えられることが期待されそうだったり、被覆面積が多く作れるところを選んでおけば後ほどブロックを縮めたい場合にも自然に対応できるだろうということ等がありました。
これは、MCTS のノード展開の時にもプレイアウトの時にも利用しています。
MCTS のノードを「ブロックの体積」「ブロックの位置」に分割
例えば、ブロックの開始位置の組が100パターン、ブロックの体積が平均的に最大20だとして、これを全パターン組み合わせて作ってしまうと2000個のノードが展開されてしまいます。前述のように、各ノードに最低数回は通さないと意味をなさないと思うと、現実的に良し悪しの比較評価をするには少し辛いです。そこで、0-indexed で 0段目をルートノードとすると、以下のように MCTS の木の深さを奇数段目と偶数段目で変えました。
- 奇数段目:ブロックの開始位置と方向だけ決める(方向は、前述のようにシルエットの被覆面積が最大の方向に固定)
- 偶数段目:ブロックの大きさだけ決める
偶数段目は4つ全ての方向が決まっていますが、奇数段目でプレイアウトをする際はブロックサイズを決める必要があるので、プレイアウトの方法と同様にして毎回ランダムにブロックサイズを決めます。こうすることで、評価値の期待値が悪そうな位置についてはブロックの大きさを調整せずに済むので、全パターン展開するよりも枝刈の度合いが高まることが期待できます。先の例でいうと、ブロックの開始位置の組100パターンのうち、有望なパターンだけ体積を調整するためのノードの展開がなされることが期待されます。
ブロックの開始位置の片方をシーンの端点に限定
各シーンでのブロックの開始位置の組を列挙する時、各シーンで原理的に置ける点を列挙すると置ける箇所が膨大になってしまい展開するノードの数が多くなってしまうため、置ける位置の組を制限したいです。
例えば、端(= シーン内で原理的に置ける位置を3次元のグリッドグラフとしてみた時、次数が小さいマス)からブロックを埋めていくような操作ができると、候補が著しく削減できて嬉しいです。しかし、ビジュアライザなどで見ても探索の過程で両シーンとも端にブロックが置かれるとは限らないため、これを採用すると多様性の面では大きく損なわれてしまいそうです。
そこで「片方のシーンは端から、もう片方のシーンは任意」という組の取り方を採用しました。これなら、1つのシーン内の探索過程には常に端の方にあるブロックは存在しますので、大きく自由度を損ねることなく組の数を削減できることが期待できます。
これは、MCTS のノード展開の時にもプレイアウトの時にも利用しています。
ブロック位置の組を、たくさんシルエットが埋められる組に限定
MCTS の奇数段目として子ノードを展開する時、ブロックの開始位置を端点に限定しても多くなってしまう場合があったので、展開するノード数が一定以上になった場合は埋められるシルエットの面積が大きい候補だけを残しました。
小さいブロックサイズの候補を削除
MCTS の偶数段目やプレイアウトの過程でブロックサイズを決める時、例えばサイズ1のブロックを選択するメリットはありません。そこで、選択するブロックサイズにも以下のような制約を設けました。
- そもそも作れる最大ブロックサイズが小さかったら、常に最大で作る
- 原理的に作れるブロックサイズが十分大きかったら、確率 p で最大サイズ、残りは最大サイズの半分から最大サイズ位まで一様ランダムにブロックサイズを選択
ブロックの各開始位置を何回かランダムに選択して、シルエットの被覆面積が多い開始位置を選択
プレイアウトの過程を観察すると、原理的に小さい体積しか作れないブロック位置をたまたま選択してしまったためにスコアが一気に悪化するようなケースが散見されました。そこで、ブロックの方向選択のように「たくさんのシルエットが被覆できるブロックが偉い」という立場に立って、非復元抽出で何回か位置選定をやり直してその中で最大面積が被覆できる場所を選びました。
ブロック構築直後、シルエットの被覆度合いが変わらない範囲でブロックの体積削減
ビジュアライザで観察すると、何もしないとシルエットが埋め終わった後で小さいブロックの体積を膨らませる際に余剰の体積が残りませんでした。可能であれば、プレイアウトの過程でシルエットを埋めつつも後に生じる小さなブロックのために余剰の空間が残った状態にしたいです。
そこで小さいブロックのへ割り当てる空間を広げるために、ブロックを一度構築した直後、シルエットを被覆できた面積が減らない範囲でブロックの BFS の探索履歴の木としての葉ノードから削除します。
離れ小島の削除
あまり該当シードは多くないのですが、シーン内部で原理的に置ける場所のグリッドグラフを考えた時に連結成分のサイズが小さい離れ小島のような場所が存在することがあります。ここにブロックの開始位置を設定してしまうとどうあがいても大きなブロックが作れないので、シーン完成が不可能にならない範囲で探索の事前に削除しました。
回転による近傍変化を事前計算
プレイアウトの際にブロックの向く方向を変えながら探索するのですが、回転行列を使って向きを作っていたのでこのままだと近傍のマスへアクセスするために行列ベクトル積を都度計算する必要があり、行列のサイズが小さいとはいえ計算が重いです。そこで、高速化とコード単純化のために以下のように探索中に回転に必要な情報の前計算をシーンごとに行いました。
- 原理的に置ける座標位置に対して番号を振る
- 以下のテーブルを事前計算する
- neighbor[p][axis][dir] := 座標に振られた番号 p について、座標の対応 24 パターンのうち axis 番目に対応する、上下左右奥手前6方向のうち dir 番目の方向に位置する座標番号
こうすることで、共通ブロックを切り出す操作の過程で3次元や回転を意識せずに実装できました。
パラメータ調整
Optuna 使って500テストケースでパラメータ調整しました。スコアに対して3~4%程度は寄与しているので、寝ている間に色々やってくれるのは本当にありがたい…
所感
- コンテスト後半で、いい感じのブロックでシーンが埋められるようになったのをビジュアライザで確認できた時はかなり嬉しかった
- 以前コンピュータービジョンを勉強していた時に回転行列を履修していたので、ここでほとんどロスなく実装できたのは結構嬉しかった
- 終始良く作られた局所探索に勝てないだろうなーと思っていたので、最後の土日は追い上げがずっと怖くてヒヤヒヤしていました
- ただし、僕が局所探索するよりは乱択貪欲の方がマシそうと思っていたので、その感覚自体は間違っていなかった気もする
- 局所破壊再構築やりたかったけどできるイメージ持てなかったのは正直悔しかったから、次に使えそうな長期コンがあったら今度こそ経験積みたい
RECRUIT 日本橋ハーフマラソン 2022夏(AHC013) 参加記
問題
成績
最終 2000 テストケースで 13,808,196 点 (平均 6904 点)、 19th / 850 でした。2回目の橙パフォ+レート黄色到達+1ページ目めでたい!
解法
自分の解法は、ざっくり以下の通りです。
- 貪欲法っぽく同じ種類のサーバを繋げて巨大な木を構成する操作を、1種類ずつ行っていく
- 2種類目以降のサーバを繋げやすくするために、最初に作る種類のサーバだけ入れない領域を作成する
- 空白が足りなくなったら、既に繋げたサーバ間の空白を消して縮める
- 木の構築開始地点、禁止領域の形、木を構築するサーバの種類の順序を色々試して最善のものを選択
以下、もう少し詳細です。
同じ種類のサーバを繋げて巨大な木を構成
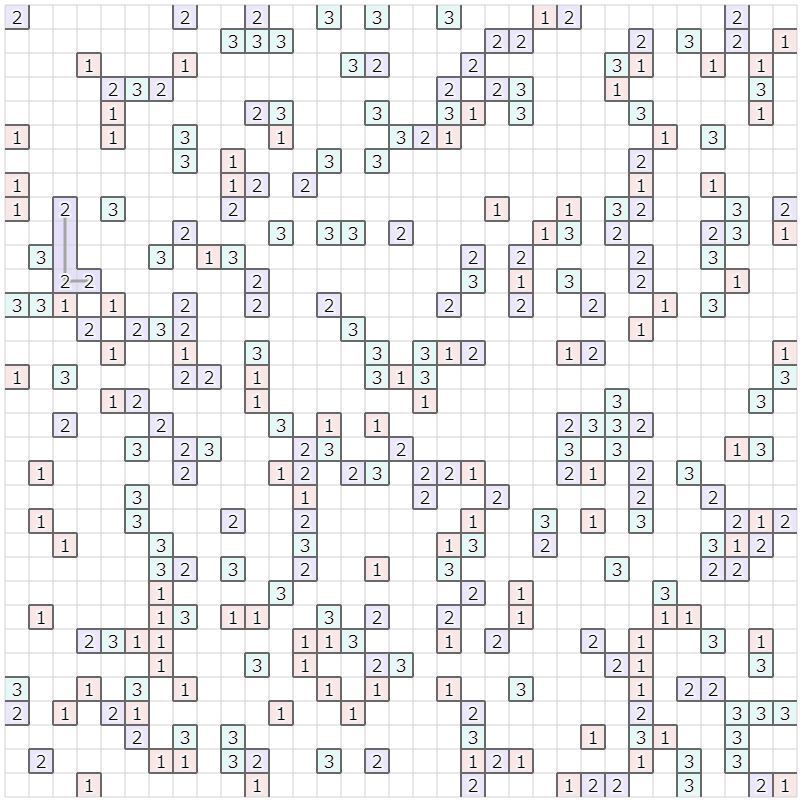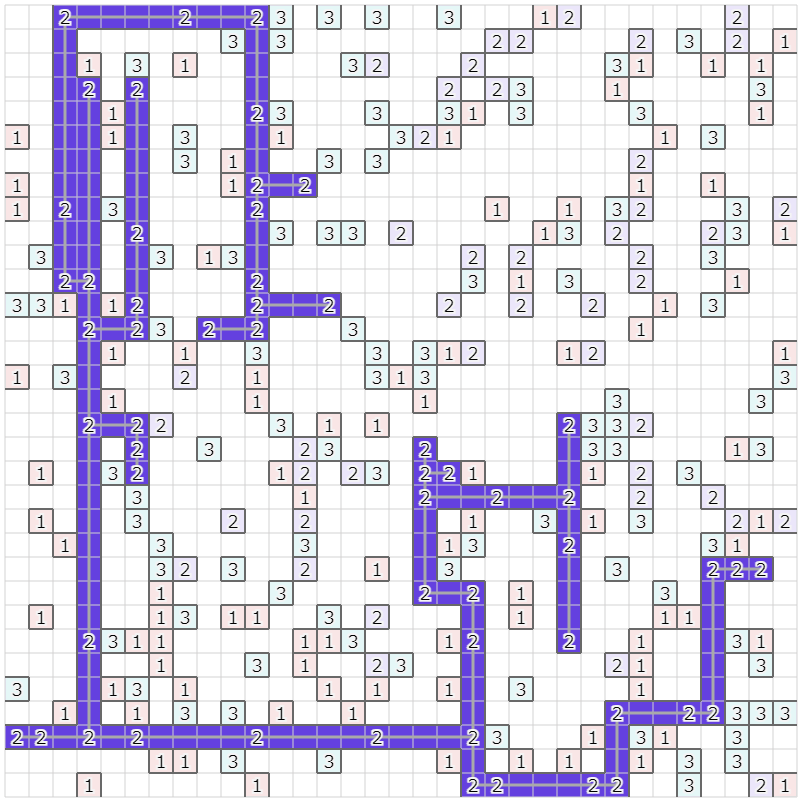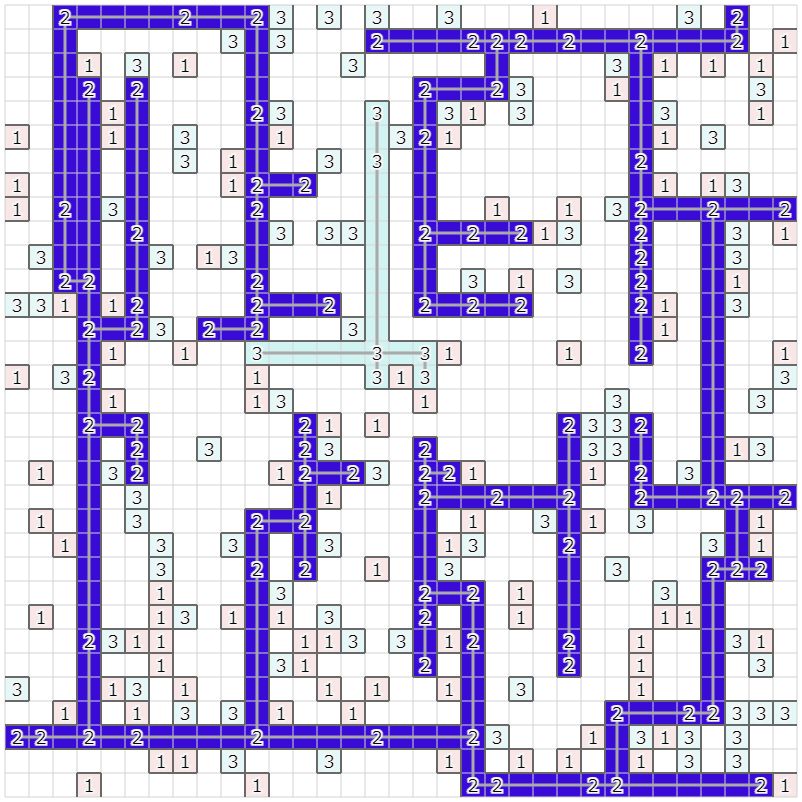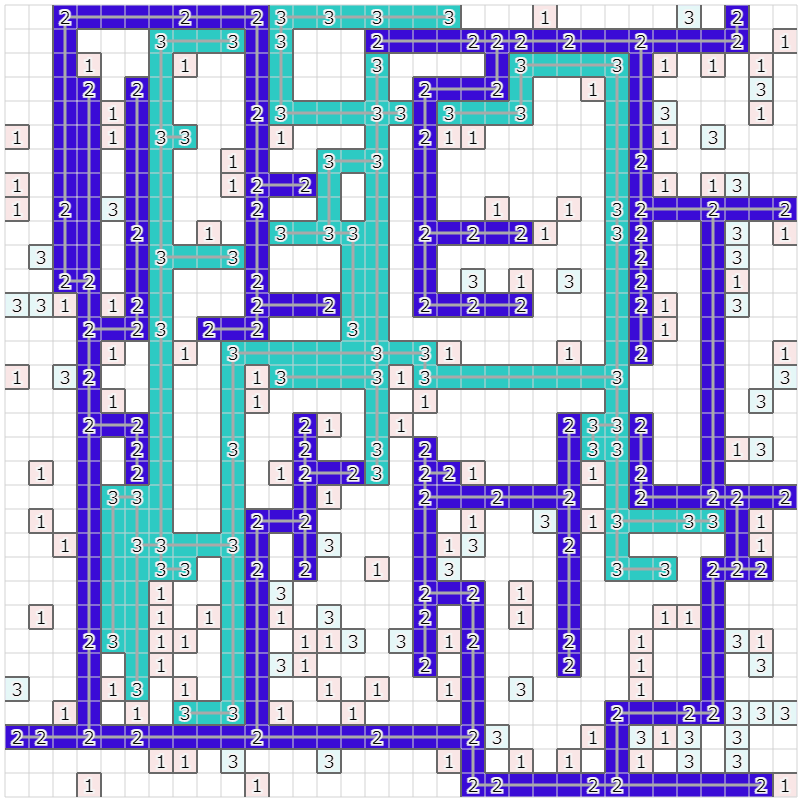
得点の計算方法から複数の小さなクラスタを作るよりも一つの大きなクラスタを作った方が高得点になりやすいため、同じ種類のサーバを100台繋げることを目指します。巨大な木を作るために、1台ずつサーバをくっつけて木を構築する方法を実装しました。
ただし、真面目にコスト計算すると処理が重いと判断して、クラスタに属するサーバと、クラスタに属さないサーバを接続するためのコストを、以下のように妥協して見積もりました。
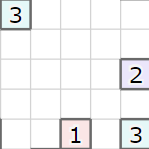
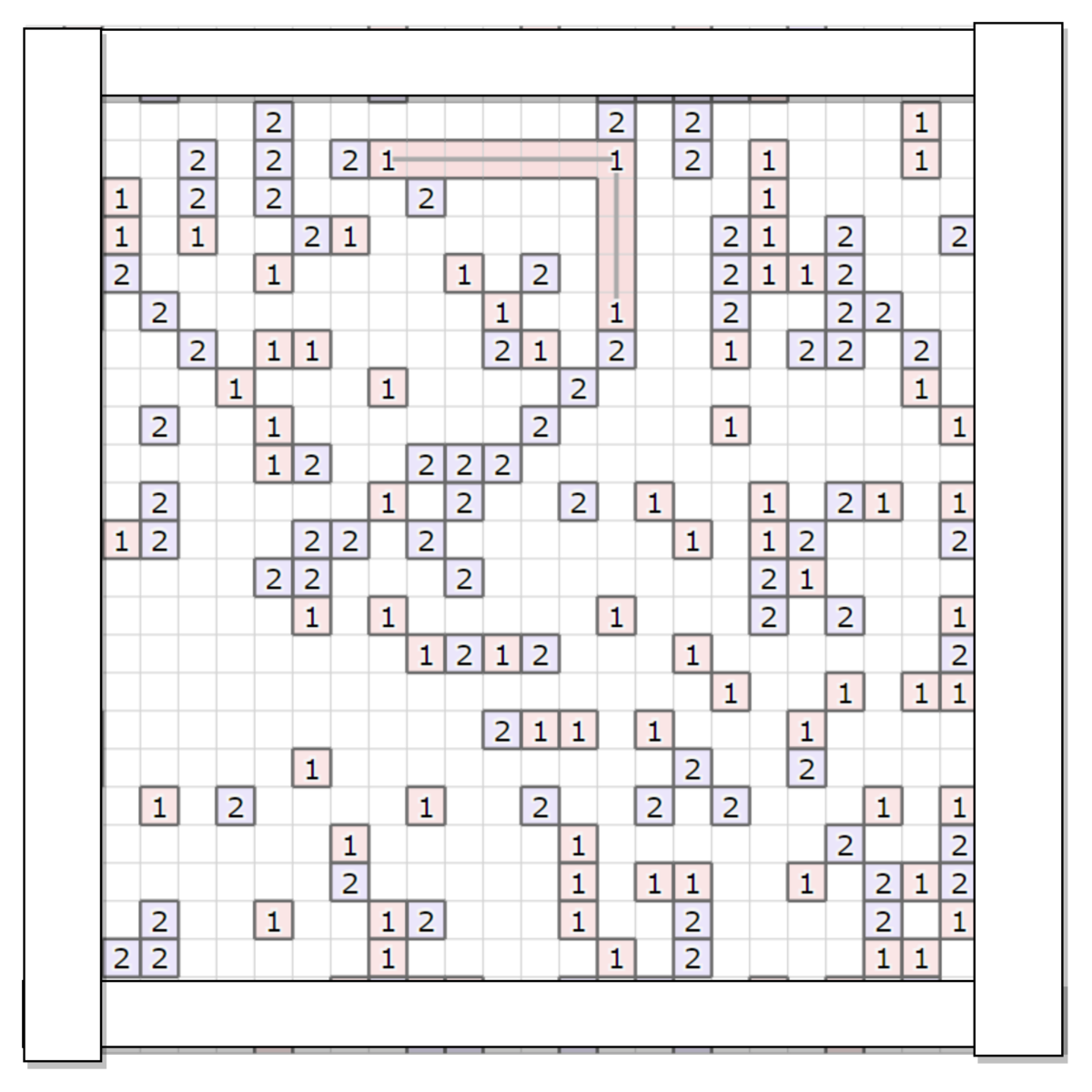
例えば、上の図で種類 "3" のサーバを接続する場合として、左上のクラスタ内に接続されたサーバを、右下のクラスタに属さないサーバに接続する例を考えてみます。この場合、
- 各サーバを上下左右に動かす範囲、かつ2サーバで構築される長方形領域内部に限定して、どの位置で接続するかを列挙する
- 各サーバを移動する軌跡および予定する接続上に存在する、種類 "3" 以外のサーバの個数を計測(邪魔なサーバ、と呼びます)
- 接続を作るためにどかす必要のある、邪魔なサーバの個数が最も少ない接続の位置を選択する
という流れで、接続位置の候補を決めます。
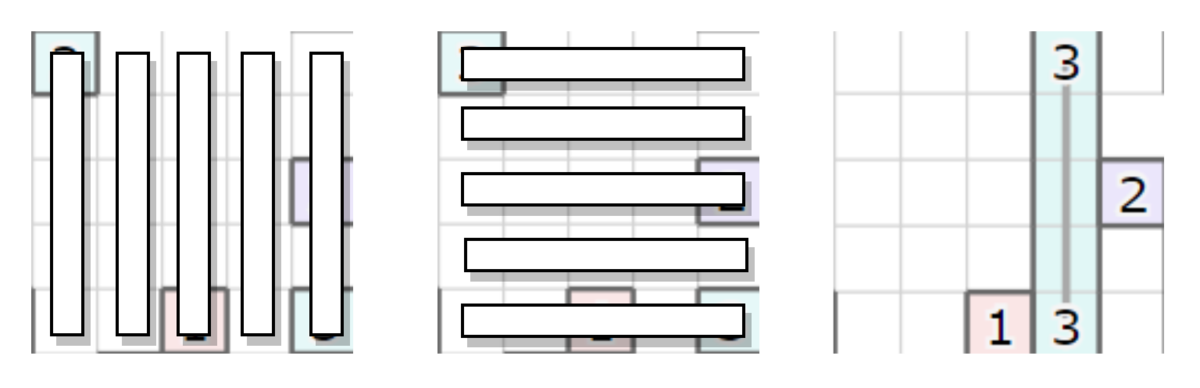
この例では上下の接続5本、左右の接続候補5本のうち、右から2番目の縦方向に接続しようとします。
ただし、結構細かな実装は割と複雑で、
- クラスタに属するサーバは、既にある接続の整合性を保ったまま動ける範囲は限られている可能性があるので、その場合はより限定された候補になりえる
- 既に同じ数字で接続が張られているところへ移動する場合は、その接続の整合性を保ったまま1マスずつ動かす関数を実装して頑張る
等を考慮する必要があります。
(クラスタに属するサーバ、クラスタに属さないサーバ)のペアは、サーバ間の $x$ 座標、$y$ 座標の差分をそれぞれ $dx, dy$ とすると、 $ \min(dx, dy) <= 3 $ に収まる範囲で全探索しました。これは、接続までに要するターン数の下限が $ \min(dx, dy) $ のためです。
実際に上記の接続を行うときは、邪魔なサーバを最も近い空白へ押しやるために毎回復元付きの BFS で邪魔なサーバをどかしています。ただし、後から全体を俯瞰した時に明らかに手損の状態もそのまま残して進んでいきます。
最初に作る種類のサーバだけ入れない領域を作成
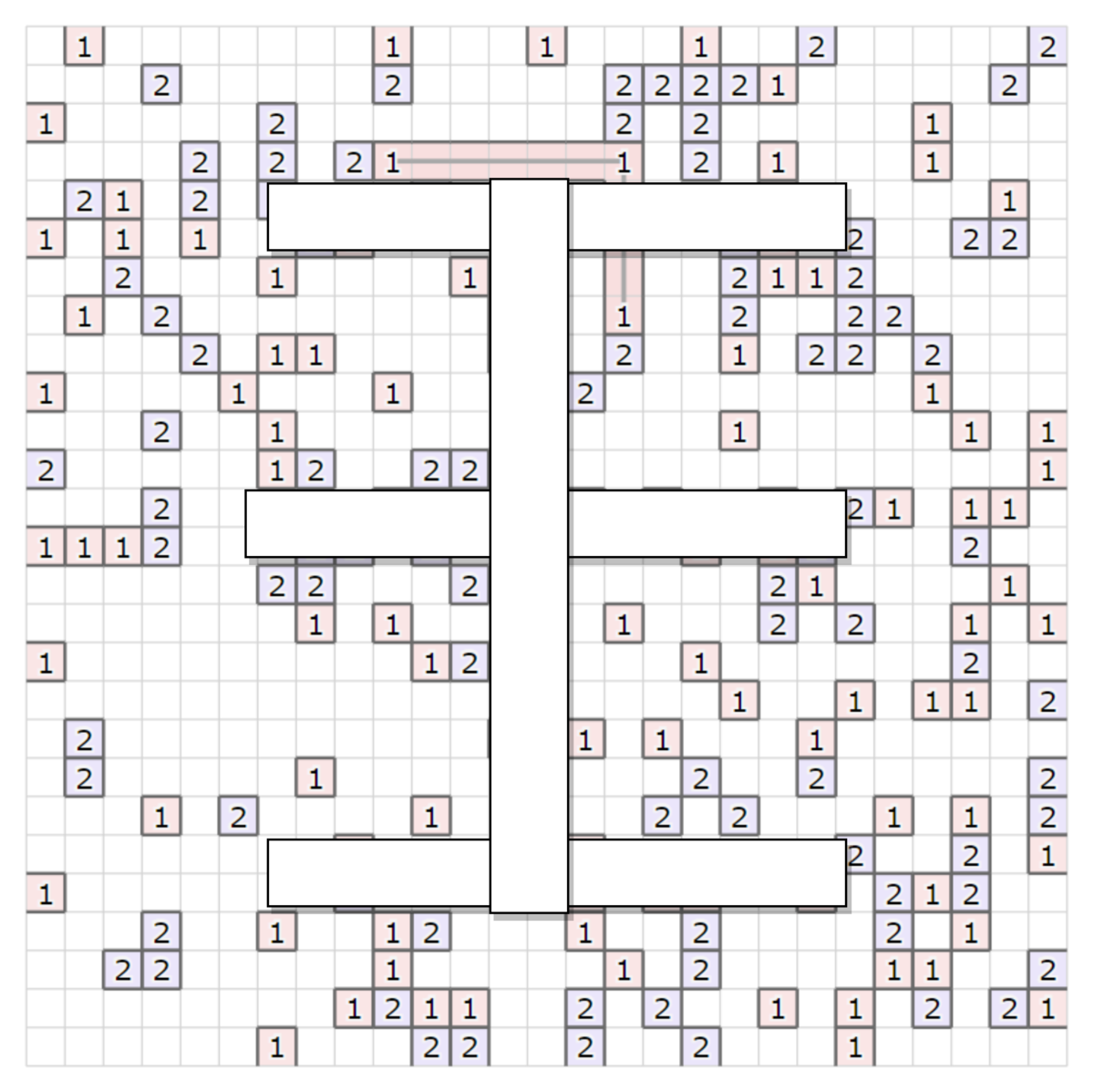
上記の方法でサーバを自由に繋げた場合、2種類目以降に作るクラスタの木のサイズが小さくなってしまったため、最初にクラスタを構築する種類のサーバだけが入れない、かつ接続の辺も張れない領域として、上記のような王の字を指定しました。例えば、1 → 2 の順にクラスタを作るとすると、1は王の字に辺も含めて入ることができないため、次にクラスタを作る種類である2の木が構築しやすいことが期待できます。王の形は、横方向に盤面サイズ/4、縦方向に4マスを空けた、幅2の王の字のみを試しました(最終的にこの形になったのは、単に時間が足りなかったからです)。
ただし、特に空白が少ない場合などでは禁止領域がない方がよい場合もあったので、全く制約を書けない場合なども試しています。
最初は上記のように周囲2マスを空けるような禁止領域を作ったのですが、開発序盤で貪欲法の探索部が弱かったことで移動量の損がかさんでしまったりしたこともあり、最終的な調整まで間に合いませんでした。王の字の形状は、周囲2マスを全部禁止にするよりも禁止領域の面積が狭くある程度全体に届くため、私の解法のように貪欲法の探索度合いが弱くても機能しやすいかなぁという気持ちで設計しました。
余談ですが、後で周囲2マスを禁止領域に指定するコードも後日追加してみたところ、それだけで50テストケースで 350,376 → 354,334 になったので、王の字で全てはカバーできていなかったようです。結果論ですが、コンテスト残り2時間の時に一番費用対効果が高かったのはこの部分だったのかもですね。
既に繋げたクラスタを縮める
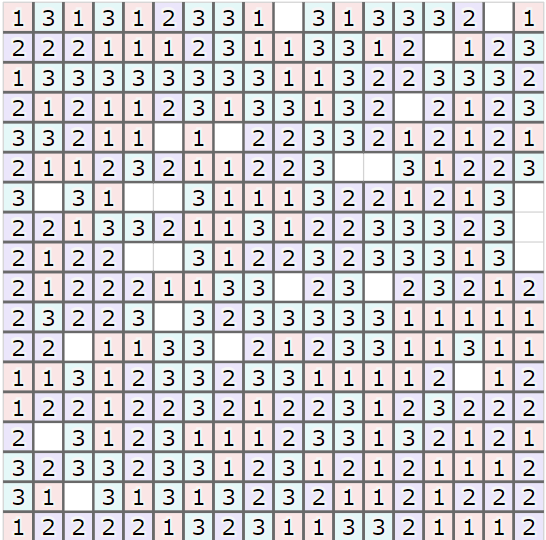
上記のように、空白が少ないテストケースだと、雑に貪欲で繋げていくとすぐに空白がないせいで手詰まりになってしまいます。そこで、手詰まりを回避するために、余計なサーバが移動不可能になったら既に繋げたサーバ間の接続の空白を見つけて縮める操作を行いました。
色々試して最善のものを選択
高速化する時間が十分とれず、1試行解を作るのに数10ms 程度必要だったので、Nが小さなテストケースでも100回程度しか試行回数が稼げませんでした。
そのため、乱数に頼って乱択せずとも、(クラスタを構築するサーバの種類の順序、最初の種類のサーバで木を構築開始する地点、禁止領域のパターン)を色々変えて一番良い解を出力するだけで十分時間を使い切ることができました。
結果の解釈
テストケース毎の分布は、wleite さんの統計情報がとても参考になりました。
終わってみれば、サーバの種類が少ない K = 2 がとても弱かったようです。クラスタを構築するための手順が全然最適化できていなかったので、雰囲気的には貪欲に繋げていく方法が限定的であったり、山登りなり焼きなましできなかった弱点が出てしまったのかなと感じています。
起きたこと(時系列)
本当にメモを取る余裕がなかったので、今回は何も書けず…
所感
- 実装に苦労したコンテストでしたが、実装に苦労した分最初に100サーバ全部繋がった時にはめちゃくちゃ嬉しかった(AHC011 や AHC008 みたいに実装が大変だった系のコンテストは結構そうなりがち)。
- 今回みたいに実装が重いコンテストは、実際にコードにバグはないけど論理的にバグがある状況になりがちなので、もう少しデバッグ周りで補助ツールを充実させたいなという気持ちになりました。これいつも言ってる気がするけど。
- 次こそこういう実装重いコンテストで焼きなましたい。こっそり練習頑張ります。
「まわしてそろえる」のコスト計算過程の備忘録
記事の概要
「まわしてそろえる」とは、第3回 RCO日本橋ハーフマラソン 本戦Bの問題です。
atcoder.jp
本記事は、以下のmaspy さんの記事を見て復習していたのですが、コストの効率的な導出をきちんと理解するために、ちゃんとゴリゴリと式展開をした過程をメモした、自分用の備忘録です。
maspypy.com
解法の概略としては「2つの領域に分ける問題」の小問題として3つに分割し、各小問題では、一部の要素に限定して$x$座標または$y$座標の総和でビームサーチをします。例えば、0~3の数字を「0または1」と「2または3」に上下で分ける時、「0または1の$y$座標の総和」がコスト関数になります。解法の細かなポイントは他にもいくらかありますが、記事の本質ではないので省略します。
上記の計算は、2次元累積和を管理することで高速化ができるのですが、きちんとその導出を自分の手で行おうとしたら詰まってしまったので、その流れをメモすることが本記事の目的です。
導出方法
本記事でやることは1つだけで、現在の解の状態から特定の領域を90度、180度、270度、1回だけ回転させた時に、どのようなコスト差分になるか計算することを目指します。以下では、例として領域$S$を$a \leq x < a + s, b \leq y < b + s$(この$x, y, s$は、問題中の操作に対応します)、$D_S$ を$S$の内部で下へ寄せたい要素(上記の例では「2または3」)、$U_S$は$S$の内部で上へ寄せたい要素(上記の例では「0または1」)とし、$p \in U_S$ に属する$y$座標の総和がどう扱われるかを書いてみます。
$Y(p): Z^2 \rightarrow Z$を、座標$p = (x, y)$から$y$を取り出す関数、同様に$X(p): Z^2 \rightarrow Z$ を座標$p = (x, y)$から$x$を取り出す関数とすると、コスト関数は以下のように書けます。
$$
\sum_{p \in U_S} Y(p)
$$
今、$p$ を$(a, b)$を起点に時計回りに90度回転させて$f(p)$に移動させる時、回転させる小領域内部で左上を原点と見なす相対座標$(x_r, y_r)$は、以下のように移ります。
$$
(x_r, y_r) \rightarrow (s - 1 - y_r, x_r)
$$
ここで、$x = a + x_r, y = b + y_r $に注意すると、最終的に$(x, y)$ は以下のように式変形して移ります。
\begin{align}
(x, y) & = (a + x_r, b + y_r ) \\\
& \rightarrow (a + s - 1 - y_r, b + x_r) \\\
& \rightarrow (a + b + s - 1 - y, b - a + x)
\end{align}
今、関数$F(V) = \{ f(p) | p \in V \}$ を、集合$V$の各要素を回転を通じて移動させる関数として、
$$
\sum_{p \in F(U_S)} Y(p)
$$
が$\sum_{p \in U_S} Y(p)$と比べてどう変化するのかを知りたいです。これは、
\begin{align}
\sum_{p \in F(U_S)} Y(p) &= \sum_{p \in U_S} Y(f(p)) \\\
&= \sum_{p \in U_S} Y(f( (x, y) )) \\\
&= \sum_{p \in U_S} Y( (a + b + s - 1 - y, b - a + x) ) \\\
&= \sum_{p \in U_S} (b - a + x) \\\
&= |U_S| (b - a) + \sum_{p \in U_S} X(p)
\end{align}
みたいなことをすると、計算が展開できます($p = (x, y)$と置き換えたのが、やや不自然かもしれません…)。同様に$X(p)$の方も頑張って展開すると$|U_S| (b + a + s - 1) - \sum_{p \in U_S} Y(p)$のような式が出てくることから、結局以下の計算が高速にできると嬉しいことがわかります。
\begin{align}
c_y &= \sum_{p \in U_S} Y(p) \\\
c_x &= \sum_{p \in U_S} X(p) \\\
c_1 &= |U_S|
\end{align}
これらの計算は、$U_S$が長方形上の領域であることを考えると、2次元の累積和を用いることで高速化できることがわかります。
また、$f$で回転させる操作を何度も適用しても同じことなので、180度、270度の回転でも同じことが言えます。$F$を通じた$(c_x, c_y)$の変化を改めて明示すると、
\begin{align}
\sum_{p \in F(U_S)} Y(p) &= |U_S| (b - a) + \sum_{p \in U_S} X(p) \\\
&= c_1 (b - a) + c_x
\end{align}
と書けるので、$c_y \rightarrow c_1(b - a) + c_x$ と移ることがわかります。同様に、
\begin{align}
\sum_{p \in F(U_S)} X(p) &= |U_S| (a + b + s - 1) - c_y \\\
\end{align}
となるので、$c_x \rightarrow c_1(a + b + s - 1) - c_y$ と移ります。
この写像を1, 2, 3回適用させると、それぞれ90度、180度、270度回転に対応するので、簡単に計算ができることがわかりました。
ここまで振り替えってみると、線形の写像しか登場しないし、わかってしまえばそれはそうだよなーという感じでしたが、結局このきちんとした導出をするために数時間溶かしてしまったので、メモを残したのでした。少し冗長な表現な気もする(例えば、わざわざ$F$のようなものを持ち出したあたり)のですが、わからなくなった時に自分が一番しっくりきた表現だったので、ここでは将来の自分のためにそのまま残しておくことにします。
Codingame Spring Challenge 2021 参加記
問題
いなにわさんのわかりやすい日本語訳があり、ありがたく利用させてもらいました。
結果
Gold 1116位でした。
もうちょっと頑張りたかったけど、何もわからなかったのでどうしようもない。
やったこと
1日単位で Action の集合を生成する beam search を 5日分やりました。
1日単位での Action の集合を列挙するために、内部で possible_action() みたいな関数をベースに wait が終了条件の BFS をしました。
Zobrist hash とか基本的な重複除去は一通り取り込んでいます。
Action の列挙の際には、以下のような Action を省く戦略を埋めました。
- completion → grow2 → grow1 → grow 0 → seed 以外の手順はやらない
- seed で種を置く対象のマスに対して、高々3か所しか木を指定しない
- 自分の木がある隣接マスには種をまかない
- 自分の木と桂馬の関係にあるマスにしか種をまかない
3, 4 つ目の条件を両方満たす位置の候補がそんなにないせいで、sun 出力が伸びなくて厳しい盤面があったりしたのだけど、単に候補列挙のルールに優先順位をつければよかったということに感想戦で気づいた。
評価関数は、最初に適当に指定した
- 最初16日: 直近6日で得られる sun の合計スコア
- 後半8日: スコア
がそのまま採用されました。色々工夫を試していたけど、結局あまり強くなってくれなかった。
所感
- 今回で3回目だったけど、1, 2 回目と比べてよりゲームの文脈で考察できるポイントが増えてきた気がする
- それに比例して強い bot が作れているわけではないのが悲しいところ
- 1, 2回目と比べて、意味不明なエラーで落ちて泣いてる時間がかなり少なかった
- これは Rust の恩恵な気がしていて(これまでは C++)、まだ実装やライブラリ選定が不慣れな分を差し引いても、かなり元が取れていると感じる
- パラメータチューニングを前提にした評価環境は最初に作りたい
- 後半で評価関数のパラメータチューニングをやろうと思った時に、時間をかけて作るのが億劫になってしまう
- コドゲのサービス上で動かすと、stderr の一部が切れて表示されないことを半年たつといつも忘れる気がするし、そもそも timeout があるから不便
- MCTS をしたい状況が体感できた。
- ルールベースの bot も書いてみていいなと思った
- 評価関数の設計や枝を刈るいい練習になる気がする
おまけ:コンテスト中のやったことメモ(時系列、自分用)
Wood 2
自分の木を選んで Complete。
Wood 1
1本ずつ Grow。
Bronze以降
実装①: 試合を見るための仮ソルバ作成
相手を無視したスコア関数を元に貪欲をして、とりあえず試合運びを確認する。 序盤は sun の最大化、終盤はスコアの最大化
考察: 自分以外の試合を見て重要そうなポイント
- 盤面の richness は、中央であるほど高いので固定らしい
- 一方で、完全に中央は日が遮られやすいので、注意が必要
- 場所の強さが mod6 で異なるので、mod6 で育てる場所を変えたい
- 中央に size 3 木を残しておいて、強い場所に1手で撒けるようにする
- 桂馬っぽいの関係で正三角形を作ると、少なくとも自分で自分を遮ることがなくて強い
- 相手のそばに置いて、相手の sun 取得を妨害するような動きができると良さそう
- 相手の木に対して、多対一で接していると、妨害効果が強そう?
- 相手から妨害される未来が見える時には得点に変換してしまうのが良い?
考察: 自分のソルバがダメそうな所
- richness が高そうな場所に seed をまいてくれない
- grow のコストが過剰に低く見積もられている
実装②: ビームサーチ化
基本的には自分のみを考慮 + 相手の行動や状態を基に若干のボーナスをつけて、ビームサーチ。 1 Action が 1ターン。
- コスト関数
- 12手以前は、それ以降で得られる sun の最大化
- 今の手持ちの sun は加えない
- 12手以降は スコアの最大化
- ボーナス①:Complete した時に、相手が次ターン以降に行うと思われる Complete の回数 / 1.5ビームサーチの手数 で加える
- 時間減衰させないと無限に後回しにする
- 相手が次ターン以降に行うと思われる Complete の回数 = max(10 - これまでに complete した回数, 相手が今持つ size 2 以上の木の個数)
- ボーナス②:Seed した時に、richness の分だけ加える
- seed を撒くにしても richness の大きさも考慮したい
- ボーナス①:Complete した時に、相手が次ターン以降に行うと思われる Complete の回数 / 1.5ビームサーチの手数 で加える
- 12手以前は、それ以降で得られる sun の最大化
- ビーム幅
- 12手以前は 400
- 12手以降は 600
- 手数
- 12手以前は 20 手
- 12手以前は 40 手
- その他
- 候補を作る際、sun が少なかったり候補手が空出ない限りは、Wait をしない
- 本当は入れたくないけど、ターン数が経過してしまうことを表現する方法が思い付かないので苦肉の策
- 重複除去として、同一の (直前ターン盤面 id, action id) を2つまでしか持たないようにした
- 候補を作る際、sun が少なかったり候補手が空出ない限りは、Wait をしない
考察: 自分のソルバがダメそうな所
- size 2 -> size 3 Grow を打ってから、Completion してる…
- Grow に対する Action Bonus はないけど、Completion に対する Action Bonus がない、かつ Action Bonus は累積しないのが問題
- 後ろで Action Bonus を選んだ方が有利になってしまうため
- Bonus を累積的にして調整するなども検討したが、結局 possible_move で直前の action も状態に持たせたうえで上記の遷移を禁止
- Grow に対する Action Bonus はないけど、Completion に対する Action Bonus がない、かつ Action Bonus は累積しないのが問題
- どうも richness の差が結構効いているように見える
- ありえないけど、全部 richness 3 のマスで木を生やせたら、めっちゃ強いよねやっぱり
- 初手の動きがかなり弱い
- 自分の動きは、地震に隣接する場所に置かないのだけど、どうも初手で中央を制圧されてしまうことが richness の差で負ける要因にもなっている気がする
- 最初は、速やかに中央を制圧するための手順を読むのがいいのかも?
アルゴリズム上の問題点
- Action を評価するのが良くなさそう
- 良いものにバイアスがかかる得点を入れるより、悪いものを選択しないようにするほうが調整が楽だし、ターン数に対するコスト値の普遍性もある
- 1 つの Action を beam search の1ターンにしているのが良くなさそう
- wait すると sun が入るので、wait を連打するのが比較的良好な戦略になってしまいやすい
- 実際、seed を撒くような数日後によくなる手は、ビーム幅が狭いこともあって全部消えてた
- wait すると sun が入るので、wait を連打するのが比較的良好な戦略になってしまいやすい
実装③: 1日単位で行うビームサーチ
- 実装簡略化のため、実装②のビームサーチの内部で、1ターンずつ進める BFS をやって、1日が終わるまでの盤面を生成する
- ビーム幅
- 100
- 手数
- 3日分
- コスト関数
- 前半16日: 直近6日で得られる SUN 値
- 後半8日: スコア
ただし、時間制限が来たら途中で終わる実装を入れていて、実際中盤などは途中で終了していた。 これでギリギリ Gold には入れた。
実装④: コスト関数の設計
ビームサーチのスコアがさすがに雑なので、visualizer を見て試行錯誤していた。
- スコア
- size 0 ~ 3 の木の本数がそれぞれ [2, 2, 2, 5] に近い
- 直近 N ターンで自分がもらえる sun の合計値 * 2 - 直近 N ターンで相手がもらえる sun の合計値
あたりを頑張って重みづけしようとしてたけど、思ったように動いてくれなかった。
AHC001 参加記
問題
結果
70 位でした。1ケースだけ TLE していたらしく、少し順位下がった。
やったこと
自明解
各広告が絶対覆う必要のある $(x_i, y_i), (x_i+1,y_i+1)$ に長方形を置くことで、必ず制約を満たす解を得られる。
自明解の改善①
コスト関数が改善する場合に自明解から上下左右に 1px ずつ拡大すると、自明解より大きくコスト改善しそう。 そこで、
- 自明解を初期状態にする
- ランダムに長方形を選択し、伸ばす方向も上下左右 1 方向をランダムに選択
- 2で定めた方向に 1px 伸ばせて、コスト関数が改善し、制約を満たしていれば採用
- 改善ができる間は 2 に戻る
- don't look bit みたいなので、近傍ひと通り見て改善しなかったら探索候補から捨てていくみたいなのをやった
- 時間いっぱいまで 1. からやり直す
をやった。点数は 458,... 程度。
Submission #20681357 - AtCoder Heuristic Contest 001
自明解の改善②
自明解の改善①で、どう見ても伝播して押せるケースがあるのがわかったので、BFS で辿って押せるか判定する処理を追加した。 点数は 478,… 程度。
考察
ここまでで得られた画像を見てみると、より煩雑な操作で改善はしそうだったけど、トップと明確な差があったので中断して考察。
- アルゴリズム選択
- 1px ずつ伸び縮みさせるより、置ける範囲で最大の長方形を置く方法を考えたい
- 制約遵守を保証し続けると動き辛いので、最初は制約違反しても OK にしたい
- 広告どうしが重なるのは OK そう
- 他の広告が含まれるべき点 $(x_i + 0.5, y_i + 0.5)$ を含むのはダメそう
- 局所解を脱出する方法は作りたい
ついて考えた。
アルゴリズム選択
ビームサーチは、ビジュアライザとにらめっこしたり、特徴量を並べても何をどういう順に置けば良さそうかがよくわからなかった。 例えば、
- (要求された広告面積 / 原理上置ける最大広告面積) が大きい順
- 広告面積が大きい順 / 小さい順
- 端から順に置く
みたいなのを考えていたけど、軽く実装して確かめた感じだと上手く行きそうになかった。
また、焼きなますのも考えてみたけど、改悪を許したとしても、十分小さい近傍では次のいい状態につながる想像が全くできなかった。 という訳で、最終的に山登り+大きめに状態を変えるような操作を時間いっぱい繰り返すことを考えた。
最大の長方形を置き直す
本当はちゃんと説明しようとしたけど、時間が経ちすぎて気力がないので省略。大まかに言うと、
- 座標圧縮
- 塗り絵みたいなことをやって、最大長方形の頂点候補を抜き出す
- その長方形に含まれるべき点からみて第一象限〜第四象限に分類
- 4重ループで全部列挙(多すぎたら適度に省略)
- 経験的には大きくならないけど、一個 TLE したのはこれが原因っぽい?
制約違反をしても OK な方法
2 広告間の面積の重なりを合計したものをペナルティとして入れ、時間と共に線形でペナルティを重くするよう設計した。 これにより、自明解②の push 操作は、重い上に自然に達成されると判断して削除した。
ペナルティを別に入れることも考えたが、共通部分で重なる箇所は面積を直接減らすことでスコアを削減すれば良さそうとわかったため、 重なりが判定された長方形は、その分スコア計算時の面積を両方で減らす方針にした。 が、実装してみたけど全く上手く行く兆しが見えずにやめた。
局所解を脱出する方法
得られた画像を見ると、一部の長方形をまるっきり別の場所に置かないとどうにもならない、というパターンがあった。 そこで、
- スコアが悪い下位5個の広告 A と、それに隣接する広告 B をランダムに選択
- 広告 A, B を 1x1 に縮める
- A をスコア最大の長方形で置き直す
- B をスコア最大の長方形で置き直す
のようにして、kick 相当の処理を入れた。これが相対的にはいい工夫で、最終的には 493... 程度まで伸びた。 小さいケースだと、大体 8,000 回位は kick が行われていたらしい。
やり残したこと
スコアがサチっているけど、変形した方がいい長方形の扱いに少し困った。が、前述の置き直すコストが少し大きめだったので結局なんにもできなかった。
所感
- バグらせはしなかったけど、最大長方形を置き直す部分の処理で無限に時間を溶かした。アルゴリズム力大事すぎる
- 結局、計算量の観点でかなり損をしていたらしい
- TLE を1ケース産んだのは反省ポイント高い
- 実はローカル 1,000 ケースだと1度も起きてなかったので、対処は少し考える必要あり
- 参加人数が多くて賑わってる1週間マラソン(実質2週間)かなり楽しい
- TL を眺めていて、最後までずっと飽きなかった
- フルで毎回参加できるかわからないけど、これからののんびり楽しみたい
- できる範囲でやったことはブログに残していきたい
- とある MM で自分が時間をかけてやった方針をなんも覚えていなかったのが、割とショックだったので
レイトレ合宿7 徒競走でやったこと
はじめに
今回のレイトレ合宿では、イベントの一環として BVH の構築/交差判定を高速化する徒競走というイベントが行われました。今いる会社的なあれで高速化に詳しくなりたいというのもありましたが、やってみるとこれがかなり楽しくて、 本題の CG 作品の提出を忘れて 取り組んでいました。そこそこ勉強込で時間をかけたので、何とか忘れないようにやったことを記したいと思います。
実際のソースコードは こちら になります。
ソースコードの規約が統一されていなかったり、部分的におかしなコードがあったりしますが、昔書いたコードを必要最低限の改変で持ってきたりしてたので、許して下さい。
ルールは、BVH の構築 + 交差判定の時間が短い人の勝ちです。
とりあえず、効果が 0 でなさそうな、やったことの概要を記すと以下のようになります。
抜け漏れはあるかもしれません。あと、どうやらどこかがバグっているらしいのですが、特定できていません…
やったこと
3次元ベクトルを Expression Template 化
最初、SIMD 化もされていないコードだったので、BVH 構築/交差判定両方で一時オブジェクト作成を削減するためにやりました。最終的に、交差判定ではどのみち一時オブジェクトは作成されないので、最終的な貢献度は薄かったかもしれません。今見ると、きちんと作ろうとして途中で投げ出した後があって面白い。
ポリゴンの当たり判定を正規化した空間でやる(名前がわからない)
Polygon の当たり判定も、もっと速い方法絶対あるだろーと思って色々ググった結果、この記事 に行き当たりました。仕組みは割と簡単で、三角形を (0, 1, 0), (0, 0, 0), (1, 0, 0) の空間に写してから当たり判定するというものです。手元では、そこそこ効果があったように見えたので、採用しました。
三角形をなさない polygon の除去
本来は高速化の意図ではありませんでしたが、上記のポリゴン当たり判定方法を採用すると、obj の一部で nan を吐きまくったため、抑制のために入れました。誤差とはいえ、多少は影響あったかもしれません。
Top Down な SAH ベースの BVH の並列構築
この記事 を色々眺めた結果、とりあえず知ってるやつをやろうということでこうなりました。構築は Task Queue を使って並列化しました。詳細はアドベントカレンダーの記事 に書いたので、興味があれば見てもらえると嬉しいです。
std::stable_partition を使った O( n log n ) 構築(nはポリゴン数)
この内容は、 Bonsai の論文 で知りました。
TopDown SAH ベースの構築をする時、(僕の理解が間違っていなければ) polygon id を管理する配列を x / y / z 軸の3つ分用意し、 x / y / z 軸のそれぞれで sort した状態を保持します。 node を left / right で分けた時、この polygon id の配列を left / right の子ノードの分に分離しつつ、それぞれの子ノードの中では x / y / z 軸で sort されている状態を保ちたいです。
例えば x 軸で bounding box を 2分割したとすると、x 軸分の polygon id の分割は容易です(あるしきい値より左が left, 右が right なので)が、y / z 軸については left / right にいるべき polygon id がごちゃごちゃしているので、これを std::stable_partition を使って分離します。x 軸の polygon id list を見れば、「特定の polygon id が left / right にいるべき」というのは容易にわかるので、各 polygon が left / right のどちらにいるべきかフラグを持たせておき、 y / z 軸の polygon id を std::stable_partition で振り分けます。この時、stable 付きのものを呼ぶと、「 left どうし、right どうしの polygon ID の順番は元の配列のソート順を保つ」という性質があるので、y / z 軸で sort された状態も保つことが出来ます。
8分木の構築 + Node の当たり判定 8並列
ソースコード(2分木の展開)
ソースコード(8 並列 intersect)
定石がよくわからなかったので、2分木を作ってから展開して8分木にしました。
node の当たり判定については、reference 実装のものをそのまま SIMD に描き起こした感じなので、もうちょっと工夫が出来たかもしれません。
8 並列当たり判定で交差した node を効率的に抜き出す
この技術的課題は、この論文で知りました。
8 並列で node の当たり判定をした後、距離順に sort して 子ノードの traverse 順序を決めたいのですが、8要素のソートは重いので、交差した個数に応じて sort を分けるのがいいと記載がありました。これを実現するためには、交差した部分の index はどれかを高速に特定する必要があります。
ここで、「子ノードの bounding box との距離が INF でない bitmask を作成して、bitmask の位置にある index を 右詰めして抜き出す」という処理だと思うと、 pdep / pext 命令が使えることに気づきます。ざっくり書くと、
- 入力:1bit x 8 の bitmask当たり判定結果
- 8bit x 8 の bitmask を作成する
- pdep で 8bit おきに bit を配置するように設定し、0xFF をかけて作る
- avx512 でも大体似たような感じでいける
- 0x0706050403020100 は、64bit の数字に index を埋め込んだもので、ここから ↑の bitmask に被るところを pext で右詰めして保存
- 3.で作られた整数は実質 8bit integer なので、32bit interger に拡張して store
- 何個当たり判定したかは、入力の popcount を数える
みたいな感じになっています。この処理も参考にしたブログがあったのですが、メモに残っていませんでした。
なお、肝心のソート用関数を個数に応じて使い分けるのは、あんまり速くならなかったので、詰めた後は std::sort してます。
Polygon の当たり判定 8並列
これは本当に 1行ずつ SIMD にするだけ。
Polygon の(メモリ配置的な)並び替え
index の間接参照みたいなのを減らすためにやりました。バグらせるのが怖かったので愚直に配列作る + copy をしました。
こういうのが他にも複数あるので、多分構築は遅かったと思います。
(補足)やったけど、効果がなかったやつ(上2つはバグってた可能性大)
Bonsai
構築が明らかに遅かった+改善の余地があったので、とりあえず Bonsai しておけばいいだろうと思って実装したのですが、部分的に手抜きして作ったせいかめちゃくちゃ交差判定が遅くなり、時間切れで諦めました。今回唯一悔やまれる点があるとすると、これのきちんとした実装が出来なかったことだと思います。
insertion based optimization
見た瞬間、これはやりてぇと思って実装しました。が、何か思うように速くならず…かつ、論文とか見ると結構構築が重そうで、終了判定タイミングも結構難しいなと思ったので、優先度をそこそこ落としてしまいました。
AVX512 化(16分木 + ポリゴン 16並列当たり判定)
ほとんど AVX2 の命令を移植するだけでしたが、AVX512 では bitmask が一部 __mmask16 のように圧縮されている形式だったので、その扱いを少し変える必要がありました。手元では全然速くならなかったので、結局諦めました。
SIMD の bitonic sort
ソートが遅いということで、子ノードの交差個数が多かったらこっちの方が速いかもなーと思って実装はしてみました。やっぱり交差するノード数の期待値の問題なのか、多少調整しても速くなったか微妙だったので、やめてしまいました。
intersectAny で leaf node を優先して当たり判定
シャドウレイを飛ばす場合などでは、 polygon に 1つでも当たったら終わりなので、距離よりも当たりやすさを優先すべきだよなぁと思っていました。というわけで、Leaf Node に当たったらそっちを優先的に調べることにしていたんですが、比較条件が複雑な割に改善ケースが少ないせいか、遅くなってしまいました。
開発過程でやったこと
visual studio のプロファイラを眺める
大体ボトルネックは全てこれで把握していました。途中 inline 展開された部分の把握が不可能だったので、もうちょっと何とかならなかったものか。
途中まで SIMD 化して残りを愚直に実装する
SIMD の処理を最初から最後まで書くと大抵 100% バグっていたので、「途中まで SIMD で書いて残りは愚直に書く」をして、愚直をどんどん減らすような方針で書いていきました。
intel intrinsics guide をざっくり眺める
https://software.intel.com/sites/landingpage/IntrinsicsGuide/
そもそも自明じゃないテーマで本格的に SIMD 高速化をするのが初めてだったので、とりあえず何ができるのかをざっくり把握することをやりました。1個ずつというのは到底出来ないので、カテゴリごとに似たような命令はすっ飛ばして、雰囲気を感じていました。
BVH の validator をたくさん書く
BVH の構築後に色々データをいじりまくっていたので、一度バグりだすと何が原因なのか特定するのは難しいです。この時、処理における事前条件/事後条件を書き出して、処理する度にチェックするコード debug build で入れてました。かなり役立ち度は高かったように思います。
開発過程でやらなかったこと
cache miss のプロファイルをとる
これは本当はやりたかったのですが、 VS 2019 でやる方法がわからず。わかる人がいたらぜひ教えて欲しいです。
BVH の visualizer とか評価尺度を見て考察する
割と定数倍高速化をしてたら終わってしまったので、BVH の構築は top-down SAH のものからほとんど進歩していませんでした。もうちょい構築の工夫を入れてたら、 SAH とか体積とか当たり判定の分布とかを真面目にとっても良かった気がします。
UT を書く
reference 実装がきっちり与えられていたので、あまり必要ではありませんでした。今回は validator があれば大体問題なかったような気がします。
最終的な速度
正確に計測するのは大変なので諦めましたが、本番環境(CUI 版) + 本番データセットの hairball で 3回計測したときの中央値を取ると、最初と最後でこれ位の差がありました。あと、embree みたいな現状最強格のやつとも比較したかったのですが、使い方がよくわからなかったので諦めました。まぁこれだけ速度差があるといっても、バグを修正しないと何とも言えないよなぁという気持ちはあります。
| build(ms) | intersect(ms) | |
|---|---|---|
| reference | 9,491 | 202,253 |
| 最終版 | 7,660 | 9,500 |
| 速度比(ref / 最終版) | 1.24 | 21.29 |
終わりに
振り返ってみると、これは本当にレイトレ合宿の参加記なのかという気持ちになってきました。とはいえ、こうしてまとめてみると、意外と頑張ったなという気持ちになってきたので、とりあえずは良かったかなと思います。初めてガチで最適化を頑張ってみましたが、同じ言語でも、これだけ違うんだなぁみたいな感慨深さはあります。
来年こそは、綺麗な絵+CUDA を頑張りたい気持ちです。
役に立つかもしれない、Task Queueの作り方
はじめに
この記事は、レイトレ合宿7 アドベントカレンダーの記事です。
様々なタスクをマルチスレッドで処理するために Task Queue を使う場合があります。 OpenMP 等のように気軽に並列化できる処理もたくさんありますが、例えば BVH を構築する場合、 この記事 内に紹介されるような Task Queue が使われることも多いかなと思います。 BVH を何種類も作ったり、他の処理でも Task Queue は使いどころがある気がします(具体的にたくさん挙げられるとは言っていない)し、可読性向上の観点からも、モジュールとしては小さいですが、独立したモジュールを作りたい気持ちになります。
Task Queue を独立したモジュールとして作ろうと思って色々考えてみると、終了条件をどう表現するかが比較的難しいポイントと感じました。 例えば、今は Queue が空でも、処理中のスレッドが新しくタスクが放り込まれるかもしれないため、Queue が空だという条件は使えません。 また、処理が終了したら迅速にスレッドを終了する必要もあるため無限ループするわけにもいかず、終了条件を記述した関数を渡すのもあまりしっくり来ませんでした。
このような時、数値で表現される進捗を queue に登録する方法だと、比較的上手く表現できそうと感じたので、紹介してみることにします。 例えば、BVH の構築であれば、Leaf Node を作成したタイミングでその Leaf Node に含まれる primitive (Polygon とか) な object の個数を進捗として報告し、最終的に進捗が BVH 構築時に渡される object の個数に到達すれば終了して良い、といった感じになります。
実装
c++ での実装例はこちらになります。TaskQueue の実装と、BVH の構築とよく似た処理を行うサンプルコードを一緒に置いておきました。 この記事を書いた環境の都合上、std::optional の代わりに boost を使っています。
例えば std::queue との差分としては、
- empty() や size() 相当の処理等はなく、進捗登録とタスク登録/取得しかできない
- front() と pop() は同時にやる
- 要素が取れる保証がないので、要素取得は optional で包む
といった感じになります。
おわりに
今回はこれ以上深追いしませんでしたが、もっといい設計はできるかもしれないので、いい方法等ありましたら教えて頂けると幸いです。また、この Queue に名前がついていたり、こんな使い方が出来そうみたいな例などあったりしたら、教えてもらえると嬉しいです。